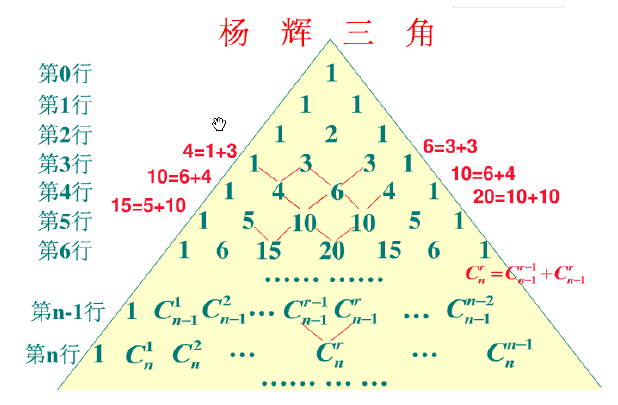
如何估算时间复杂度
首先:
常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n^2)<Ο(n^3)<…<Ο(2^n)<Ο(n!)
时间复杂度可以简单理解为最多执行次数。
一、O(1)
一般情况下没有其他循环和递归调用,时间复杂度一般都是O(1)。比如下面这样的代码
#include<iostream>
using namespace std;
int main(){
int a=0,b=0,x=0,y=0;
cin>>a>>b;
x=a+b;
y=a-b;
if(x>y){
cout<<x;
}else{
cout<<y;
}
return 0;
}二、O(n)
一般情况下,一个循环的时间复杂度是O(n),多个循环并列也是取循环次数最多的那个作为时间复杂度。当数据量增大n倍,耗时增大n倍。
#include<iostream>
using namespace std;
int main(){
int a=n;
cin>>n;
for(int i=0;i<n;i++){
cout<<i;
}
return 0;
}三、O(n2)、O(n*m)
双重循环嵌套一般就是O(n2)。当数据量增大n倍,耗时增大n方倍。
#include<iostream>
using namespace std;
int main(){
int n=0;
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cout<<i;
}
}
return 0;
}如果循环嵌套外层循环是n,内层循环是m。
#include<iostream>
using namespace std;
int main(){
int n=0,m=0;
cin>>n>>m;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cout<<i;
}
}
return 0;
}这个时候的时间复杂度是O(n*m)。
四、O(logn)
当数据增大n倍时,耗时增大logn倍。
#include<iostream>
using namespace std;
int main(){
int n=0;
cin>>n;
for(int i=0;i<n;i++){
i*=2;
cout<<i;
}
return 0;
}本来循环次数是n,现在i*=2了。那么答案是log(2)(n)。
反着想也可以,原来循环n次,现在每次i变成原来的2倍,也就是2的k次方等于n。那么正好就是log(2)(n),即O(log n)
或者下面这样:
#include<iostream>using namespace std;
int main(){
int n=0;
cin>>n;
while((n=n/2)>0){
cout<<n;
}
return 0;
}时间复杂度也是O(logn)
五、O(nlogn)
一般归并排序和堆排序是O(nlogn)。
常见的是外层循环的时间复杂度是n,内层循环的时间复杂度是logn。
比如下面这样:
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j+=i)
{
..... //复杂度为O(1);
}
}注意:外层循环是n,内层循环j每次都增加i。
常见算法的时间复杂度
| 数据结构 | 时间复杂度 | 最坏情况下的辅助空间复杂度 | ||||
|---|---|---|---|---|---|---|
| 最佳 | 平均 | 最差 | 最差 | |||
| 快速排序 | 数组 | O(n log(n)) | O(n log(n)) | O(n^2) | O(n) | |
| 归并排序 | 数组 | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) | |
| 堆排序 | 数组 | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) | |
| 冒泡排序 | 数组 | O(n) | O(n^2) | O(n^2) | O(1) | |
| 插入排序 | 数组 | O(n) | O(n^2) | O(n^2) | O(1) | |
| 选择排序 | 数组 | O(n^2) | O(n^2) | O(n^2) | O(1) | |
| 桶排序 | 数组 | O(n+k) | O(n+k) | O(n^2) | O(nk) | |
| 基数排序 | 数组 | O(nk) | O(nk) | O(nk) | O(n+k) | |
| 算法 | 数据结构 | 时间复杂度 | 空间复杂度 | |||
|---|---|---|---|---|---|---|
| 平均 | 最差 | 最差 | ||||
| 深度优先搜索 (DFS) | Graph of |V| vertices and |E| edges | - | O(|E| + |V|) | O(|V|) | ||
| 广度优先搜索 (BFS) | Graph of |V| vertices and |E| edges | - | O(|E| + |V|) | O(|V|) | ||
| 二分查找 | Sorted array of n elements | O(log(n)) | O(log(n)) | O(1) | ||
| 穷举查找 | Array | O(n) | O(n) | O(1) | ||
| 最短路径-Dijkstra,用小根堆作为优先队列 | Graph with |V| vertices and |E| edges | O((|V| + |E|) log |V|) | O((|V| + |E|) log |V|) | O(|V|) | ||
| 最短路径-Dijkstra,用无序数组作为优先队列 | Graph with |V| vertices and |E| edges | O(|V|^2) | O(|V|^2) | O(|V|) | ||
| 最短路径-Bellman-Ford | Graph with |V| vertices and |E| edges | O(|V||E|) | O(|V||E|) | O(|V|) | ||
| 据结构 | 时间复杂度 | 空间复杂度 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 平均 | 最差 | 最差 | |||||||
| 索引 | 查找 | 插入 | 删除 | 索引 | 查找 | 插入 | 删除 | ||
| 基本数组 | O(1) | O(n) | - | - | O(1) | O(n) | - | - | O(n) |
| 动态数组 | O(1) | O(n) | O(n) | O(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
| 单链表 | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| 双链表 | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| 跳表 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| 哈希表 | - | O(1) | O(1) | O(1) | - | O(n) | O(n) | O(n) | O(n) |
| 二叉搜索树 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| 笛卡尔树 | - | O(log(n)) | O(log(n)) | O(log(n)) | - | O(n) | O(n) | O(n) | O(n) |
| B-树 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| 红黑树 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| 伸展树 | - | O(log(n)) | O(log(n)) | O(log(n)) | - | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL 树 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
扫描二维码推送至手机访问。
版权声明:本文由青少年编程知识记录发布,如需转载请注明出处。