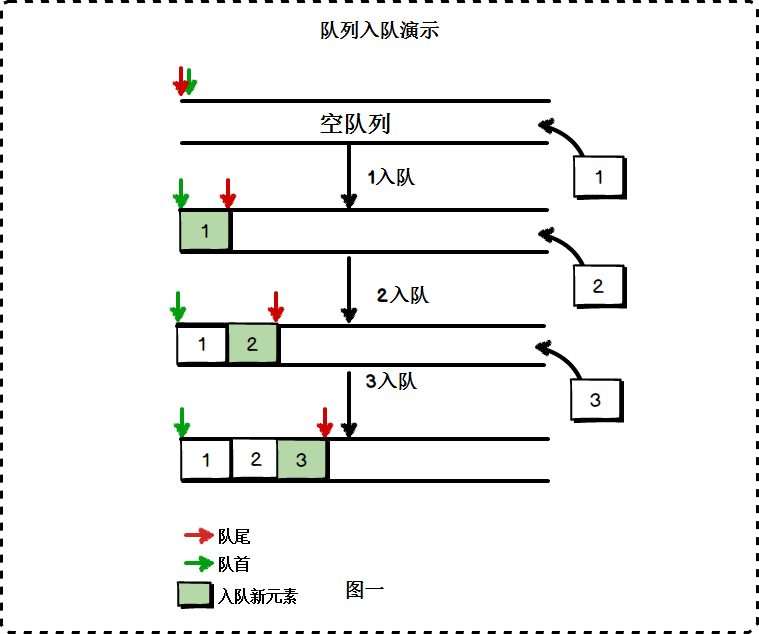
图的访问与遍历-广度优先搜索
对于无向图的广度优先搜索
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// 广度优先遍历核心函数
void BFS(int start, const vector<vector<int>>& adjList) {
// 边界检查:起始节点超出范围
if (start < 0 || start >= adjList.size()) {
cout << "起始节点无效!" << endl;
return;
}
vector<bool> visited(adjList.size(), false); // 记录节点是否被访问
queue<int> q; // 队列
// 初始化:将起始节点入队并标记为已访问
q.push(start);
visited[start] = true;
cout << "BFS遍历结果: ";
// 队列非空时循环
while (!q.empty()) {
int node = q.front(); // 取出队首节点
q.pop(); // 队首节点出队
cout << node << " "; // 输出当前节点
// 遍历当前节点的所有邻接节点
for (int neighbor : adjList[node]) {
if (!visited[neighbor]) { // 未访问过的邻接节点
visited[neighbor] = true; // 标记为已访问
q.push(neighbor); // 入队
}
}
}
cout << endl;
}
//创建邻接表
vector<vector<int>> createAdjList(int numVertices) {
return vector<vector<int>>(numVertices);
}
// 添加无向边
void addUndirectedEdge(vector<vector<int>>& adjList, int u, int v) {
adjList[u].push_back(v);
adjList[v].push_back(u);
}
int main() {
// 构建无向图示例
int vertexNum = 5; // 5个顶点(0-4)
auto adjList = createAdjList(vertexNum);
// 添加边:0-1, 0-2, 1-3, 1-4, 2-4
addUndirectedEdge(adjList, 0, 1);
addUndirectedEdge(adjList, 0, 2);
addUndirectedEdge(adjList, 1, 3);
addUndirectedEdge(adjList, 1, 4);
addUndirectedEdge(adjList, 2, 4);
// 执行BFS(从0号节点开始)
BFS(0, adjList);
return 0;
}2.对于非联通图的广度优先搜索
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
const int MAX_VERTEX = 100; // 最大顶点数
vector<int> adj[MAX_VERTEX]; // 邻接表
bool visited[MAX_VERTEX]; // 访问标记
int vertex_count; // 顶点总数
// 初始化图
void initGraph(int n) {
vertex_count = n;
for (int i = 0; i < n; ++i)
adj[i].clear();
memset(visited, false, sizeof(visited));
}
// 添加无向边
void addEdge(int u, int v) {
adj[u].push_back(v);
adj[v].push_back(u);
}
// 广度优先遍历
void bfs(int start) {
queue<int> q;
q.push(start);
visited[start] = true; // 标记已访问
while (!q.empty()) {
int curr = q.front();
q.pop();
cout << curr << " "; // 出队时输出
// 遍历当前顶点的所有邻接顶点
for (int neighbor : adj[curr]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
q.push(neighbor); // 未访问的邻接点入队
}
}
}
}
// 全图遍历函数
void traverseAll(void (*traverseFunc)(int)) {
memset(visited, false, sizeof(visited)); // 重置访问标记
// 遍历所有顶点,处理非连通分量和孤点
for (int i = 0; i < vertex_count; ++i) {
if (!visited[i]) {
traverseFunc(i); // 对每个连通分量/孤点执行BFS
}
}
cout << endl; // 遍历完成后换行
}
int main() {
// 1. 初始化图(6个顶点:0-5,其中5是孤点)
initGraph(6);
// 2. 构建含孤点的非连通图:
// 连通分量1:0-1-2(互相连通)
addEdge(0, 1);
addEdge(0, 2);
addEdge(1, 2);
// 连通分量2:3-4(互相连通)
addEdge(3, 4);
// 顶点5:无任何边(孤点)
// 3. 直接调用BFS(仅遍历起始顶点1所在的连通分量:0-1-2)
cout << "仅遍历顶点1所在连通分量:";
bfs(1);
cout << endl;
// 4. 调用traverseAll(遍历全图:包括所有连通分量+孤点)
cout << "traverseAll遍历全图(含孤点):";
traverseAll(bfs);
return 0;
}扫描二维码推送至手机访问。
版权声明:本文由青少年编程知识记录发布,如需转载请注明出处。