一、基本思想

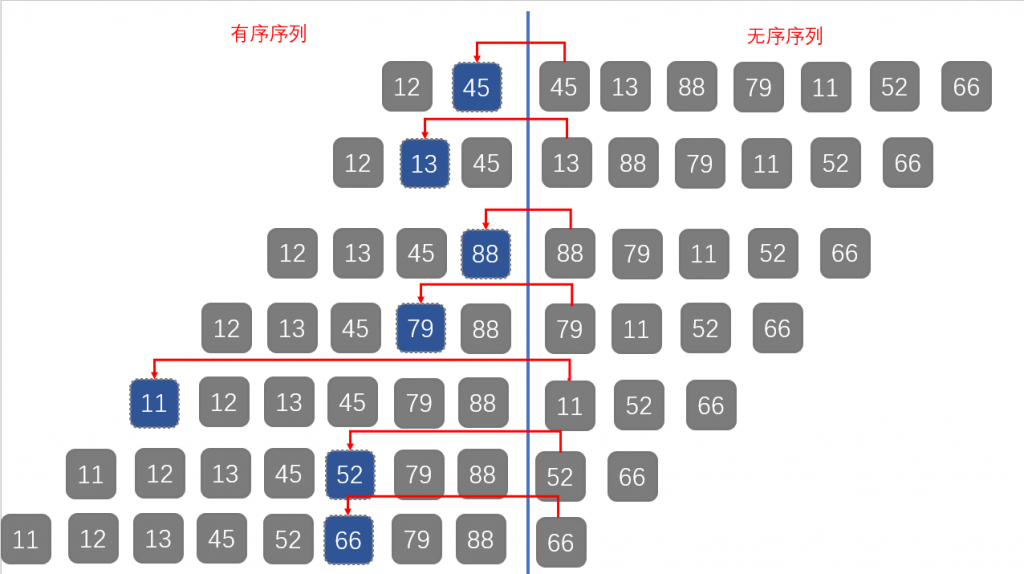
归并排序的核心思想是将两个已经有序的子序列合并成一个有序序列。整个过程分为两个主要步骤：

 1.分解：将待排序的序列不断二分，直到每个子序列只包含一个元素（此时自然有序） 

 2.合并：将两个有序的子序列合并为一个有序序列

注意1：若将两个有序表合并成一个有序表，称为2-路归并。

注意2：归并排序则类似于二叉树的后序遍历：它会持续划分区间，直到区间内元素有序，然后利用额外空间对元素进行排序，并将它们合并回原区间，直至整个序列有序。这个过程中，划分区间相当于达到树的最底层，而归并排序则相当于从树的底层开始向上遍历。

二、算法步骤

1.分解阶段：

• 将长度为n的序列分成两个长度为n/2的子序列

• 递归地对这两个子序列进行归并排序

• 直到子序列长度为1（此时已经有序）

2.合并阶段：

• 申请空间，大小为两个已排序子序列之和

• 设定两个指针，分别指向两个子序列的起始位置

• 比较两个指针所指的元素，选择较小的放入合并空间，并移动指针到下一位置

• 重复上一步直到某一指针超出子序列范围

• 将另一子序列的剩余元素直接复制到合并序列的末尾

动图如下：

三、时间复杂度

• 最优情况：O(n log n)

• 最坏情况：O(n log n)

• 平均情况：O(n log n)

归并排序的时间复杂度始终是O(n log n)，因为它总是将序列分成两半，需要进行log₂n次分解，每次合并操作的时间复杂度为O(n)。

四、空间复杂度

归并排序需要额外的空间来存储临时合并的数组，因此其空间复杂度为O(n)。

五、稳定性

归并排序是稳定的排序算法，因为在合并过程中，当两个元素相等时，可以保证左边的元素先被放入结果数组中。

六、优缺点

优点：

• 时间复杂度稳定为O(n log n)

• 适用于大规模数据排序

• 稳定排序算法

缺点：

• 需要额外的存储空间（非原地排序）

• 对于小规模数据排序效率可能不如简单排序算法

【参考代码】

// s - 当前子序列的起始下标
// t - 当前子序列的结束下标
//a[]：待排序的原始数组（全局变量）
//r[]：临时数组，用于合并时存储中间结果（全局变量）
void msort(int s,int t){
	// 递归终止条件：当子序列只有一个元素时直接返回 
	if(s==t)
		return;
	int mid =(s+t)/2;
	msort(s,mid);  //分解左序列 
	msort(mid+1,t); //分解右序列
	
	int i=s;// 左序列起始指针
    int j = mid + 1; // 右序列起始指针
    int k = s;      // 临时数组的指针
	// 比较两个子序列的元素，按顺序放入临时数组
	while(i<=mid && j<=t){
        if(a[i] < a[j]) {  // 左序列元素较小
            r[k] = a[i];   // 放入临时数组
			k++;
			i++; 
        } else {           // 右序列元素较小
            r[k] = a[j];   // 放入临时数组
			k++;
			j++;
		}
	} 
    // 处理左序列剩余元素（如果有）
	while(i<=mid){
		r[k]=a[i];
		k++;
		i++;
	} 
    // 处理右序列剩余元素（如果有）
	while(j<=t){
		r[k]=a[j];
		k++;
		j++;
	} 
	// 将排序好的临时数组复制回原数组
	for(int i=s;i<=t;i++){
		a[i]=r[i];
	}
	
}