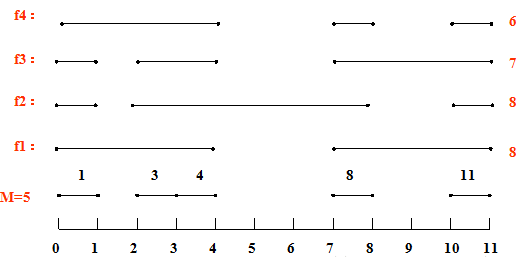
如下图所示，我们把边带有权值的图称为带权图。

边的权值可以理解为两点之间的距离。一张图中任意两点间会有不同的路径相怜。最短路径就是指连接两点的这些路径中最短的一条。

【注意】边的权值可以为负。当出现负边权时，有些算法不适用。

Floyed-Warshall算法

    简称Floyed（弗洛伊德）算法，是最简单的最短路径算法，可以计算出图中任意两点间的最短路径。Floyed的时间复杂度是N³，适用于出现负边权的情况。

【算法描述】

（a）初始化：点u、v如果有边相怜，则dis[u][v]=w[u][v]

         如果不相连，则dis[u][v]=0x7fffffff( 即INT_MAX)

  (b) 

for(k=1;k<=n;k++)
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
			if(dis[i][j]>dis[i][k]+dis[k][j]){
				dis[i][j]=dis[i][k]+dis[k][j] 
			}

（c）算法结束：dis[i][j]得出的就是从i到j的最短路径。

【算法分析】

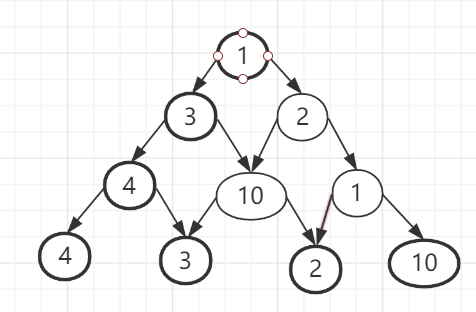
三层循环，第一层循环中间点k，第二、第三层循环起点终点i，j，算法的思想很容易理解：如果点i到点k的距离加上点k到点j的距离小于原先点i到点j的距离，那么就用这个更短的路径长度来更新原先点i到点j的距离。

在上图中，因为dis[1][3]+dis[3][2]<dis[1][2]，所以就用dis[1][3]+dis[3][2]来更新原先1到2的距离。

我们初始化时，把不相连的点之间的距离设为一个很大的数，不妨看作这两点相隔很远，如果两者之间有最短路径的话，就会更新成最短路径的长度。

【算法边形】

    如果是一个没有边的权的图，把相怜的两点间的距离设为dis[i][j]=true，不相连的两点设为dis[i][j]=false，用Floyed算法变形：

for(k=1;k<=n;k++)
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
			dis[i][j]=dis[i][j]||(dis[i][k] && dis[k][j])

用这个方法可以判断一张图中的两点是否相连。

注意：用来循环中间点的变量k必须放在最外层一层循环。