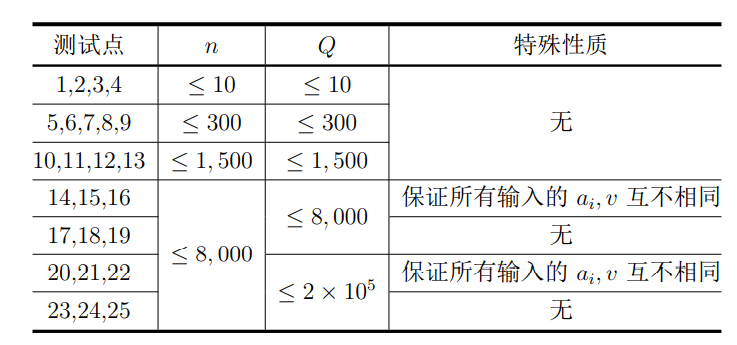
拓扑排序
一、定义
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
通俗地说,拓扑排序就是由某个集合上的一个偏序得到该集合上的一个全序的操作。
二、拓扑排序方法
(1)在有向图中选一个没有前驱的顶点且输出
(2)从图中删除该顶点和所有以他为尾的弧
(3)重复上述步骤,直到所有的顶点均已输出,或者当图中不存在无前驱的顶点为止。
比如下面这个图:
首先选取了没有前驱的顶点A,把它和以它为尾的弧删除后剩下的图如下:
再从中选取一个没有前趋的顶点。这里选择BCD都可以,我们假设选取的是B,那么删除这个顶点和以他为尾的弧,结果如下:
再从中选取一个没有前趋的顶点,选择C和D都可以,假设选取的是C,那么删除这个顶点和以它为尾的弧,结果如下:
从上面图中再选取一个没有前趋的顶点,选择D,然后把D和以D为尾的弧全部删除,结果如下:
最后剩下一个顶点E,那么其中一种拓扑排序就是ABCDE。
扫描二维码推送至手机访问。
版权声明:本文由青少年编程知识记录发布,如需转载请注明出处。